李宏毅机器学习——神经网络设计技巧
1 鞍点(Saddle Point)
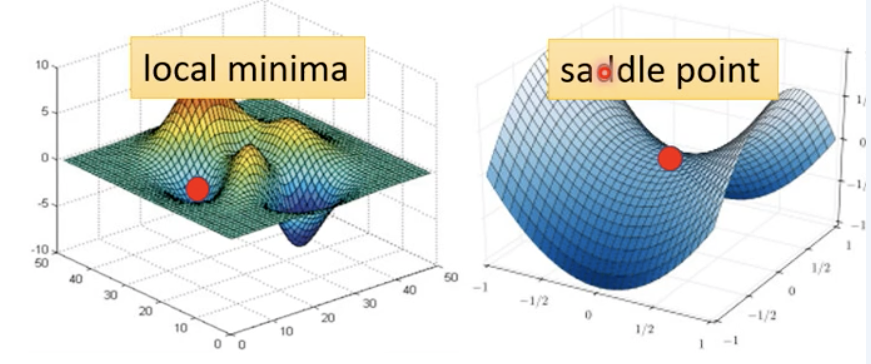
神经网络中,Gradient为0(或不存在)的点称为临界点(critical point),其有两种可能性:局部极小(local minima)和鞍点(saddle point)。
长期以来,人们普遍认为,神经网络优化问题困难是因为较大的神经网络中包含很多局部极小值,使得算法容易陷入到其中某些点。2014年的一篇论文中提出高维非凸优化问题之所以困难,是因为存在大量的鞍点而不是局部极值。
鞍点:
- 一个维度向上倾斜且另一维度向下倾斜的点。这些鞍点通常被相同误差值的平面所包围,这使得算法陷入其中很难脱离出来,因为梯度在所有维度上接近于零
- 梯度等于零,在其附近Hessian矩阵有正的和负的特征值,行列式小于0,即是不定的。
在鞍点附近,基于梯度的优化算法会遇到较为严重的问题:鞍点处的梯度为零,鞍点通常被相同误差值的平面所包围(这个平面称为Plateaus,Plateaus是梯度接近于零的平缓区域,会降低神经网络学习速度),在高维的情形,这个鞍点附近的平坦区域范围可能非常大,这使得SGD算法很难脱离区域,即可能会长时间卡在该点附近(因为梯度在所有维度上接近于零)。
在鞍点数目极大的时候,这个问题会变得非常严重。高维非凸优化问题之所以困难,是因为高维参数空间存在大量的鞍点。
鞍点和局部极小值相同的是,在该点处的梯度都等于零,不同在于在鞍点附近Hessian矩阵是不定的(行列式小于0),而在局部极值附近的Hessian矩阵是正定的。
Hessian矩阵是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。可用于判定多元函数的极值。
$$
H(f)=\left[\begin{array}{cccc}
\frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \
\frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \
\vdots & \vdots & \ddots & \vdots \
\frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}}
\end{array}\right]
$$
- 当函数的Hessian矩阵在梯度为零的位置上的特征值全为正(正定矩阵)时,该函数得到局部最小值。
- 当函数的Hessian矩阵在梯度为零的位置上的特征值全为负(负定矩阵)时,该函数得到局部最⼤值。
- 当函数的Hessian矩阵在梯度为零的位置上的特征值有正有负(不定矩阵)时,该函数得到鞍点。
2 批次和动量(Batch and Momentum)
2.1 Batch
批梯度下降(Batch gradient descent,BGD)遍历全部数据集算一次损失函数,然后算函数对各个参数的梯度,然后更新梯度。BGD的优点在于由全数据集确定的方向能够更好地代表样本总体,如果函数为凸函数,BGD一定能得到全局最优。其缺点在于每更新一次参数都要把数据集里的所有样本都看一遍,计算量开销大,计算速度慢。
随机梯度下降(stochastic gradient descent,SGD)每看一个数据就算一下损失函数,然后求梯度更新参数,这个称为随机梯度下降。SGD方法速度比较快,但是由于单个样本并不能代表全体样本的趋势,所以其收敛性能不太好,遇上噪声则容易陷入局部最优解,也可能在最优点附近晃来晃去,收敛不到最优点。两次参数的更新也有可能互相抵消掉,造成目标函数震荡的比较剧烈。
小批量梯度下降(mini-batch gradient descent,mini-batch GD)每次选取一定数目(mini-batch)的样本组成一个小批量样本,然后用这个小批量来更新梯度。每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果,可以提高算法稳定性。
2.2 Momentum
动量梯度下降法(Gradient descent with Momentum)或者叫做Momentum,通过计算梯度的指数加权平均数,并利用该梯度更新权重。
其每一次梯度下降都会有一个之前的速度的作用,如果这次的方向与之前相同,则会因为之前的速度继续加速;如果这次的方向与之前相反,则会由于之前存在速度的作用不会产生一个急转弯。简而言之,Momentum对原始梯度做了修正和平滑,具有更快的收敛速度。
3 自动调整学习速率(Adaptive Learning rate)
2.1 AdaGrad
设置全局学习率之后,每次通过全局学习率逐参数的除以历史梯度平方和的平方根,使得每个参数的学习率不同,可以使参数空间更为平缓的方向,会取得更大的进步(因为平缓,所以历史梯度平方和较小,对应学习下降的幅度较小),并且能够使得陡峭的方向变得平缓,从而加快训练速度。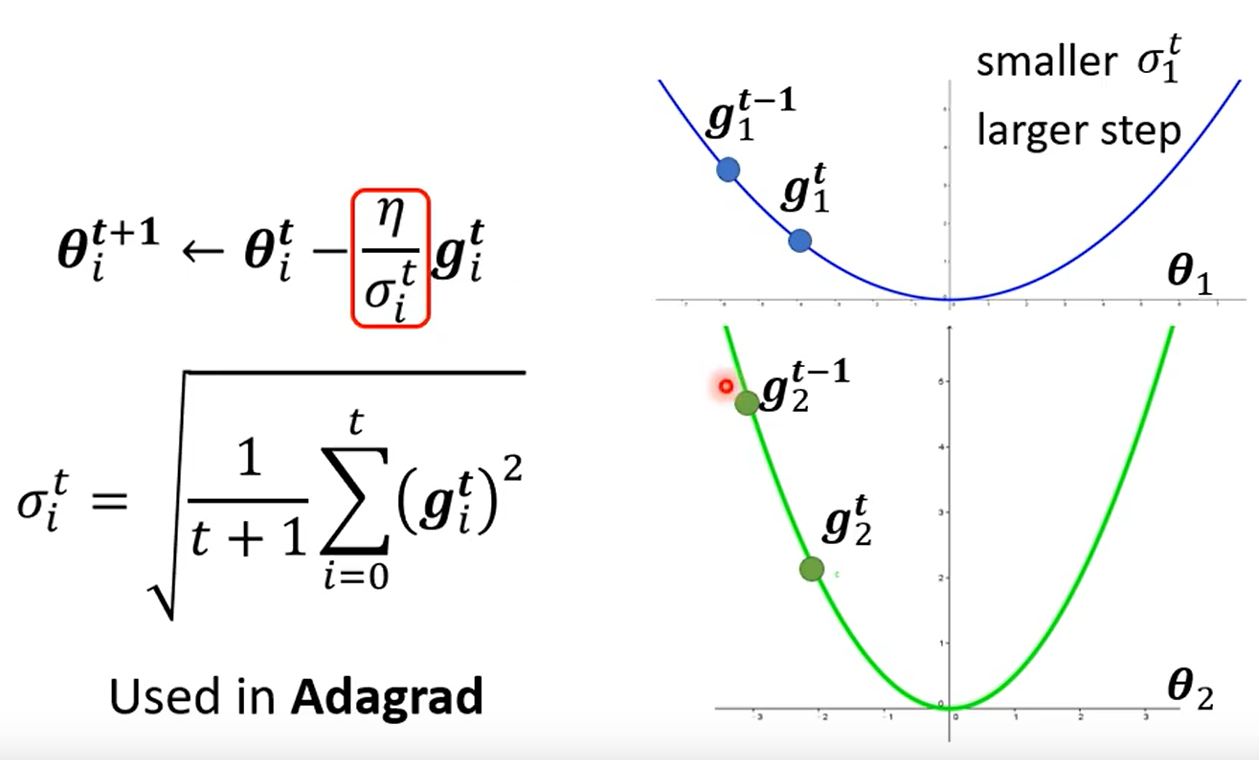
2.2 RMSprop
Adagrad会记录过去所有梯度的平方和。因此,学习越深入,更新的幅度就越小。实际上,如果无止境地学习,更新量就会变为0,完全不再更新。为了改善这个问题,可以使用 RMSProp方法。RMSProp方法并不是将过去所有的梯度一视同仁地相加,而是逐渐地遗忘过去的梯度,在做加法运算时将新梯度的信息更多地反映出来。这种方法也被称为“指数移动平均”,呈指数函数式地减小过去的梯度的尺度。
RMSProp算法不是像AdaGrad算法那样暴力直接的累加平方梯度,而是加了一个衰减系数来控制历史信息的获取多少。相比于AdaGrad的历史梯度$r \leftarrow r+g \odot g$,RMSProp增加了一个衰减系数来控制历史信息的获取多少:$r \leftarrow \rho r+(1-\rho) \boldsymbol{g} \odot \boldsymbol{g}$。
第一个等式类似Momentum,计算了梯度平方的指数平均;第二个等式根据指数平均决定步幅大小,初始化学习率η,接着除以平均数;第三个等式是权重更新步骤。其中超参数ρ一般取0.9,ε一般取1e-10。
RMSProp隐式地应用了模拟退火。在向最小值移动的过程中,RMSProp会自动降低学习步幅,以免跳过最小值。
2.3 Adam
Adam(Adaptive Moment Estimation)相当于RMSprop+Momentum,
等式1和等式2计算了梯度的指数平均和梯度平方的指数平均;等式3在学习率上乘以梯度的平均(类似动量),除以梯度平方平均的均方根(类似RMSProp),得出学习步幅;等式4是权重更新步骤。其中超参数β1一般取0.9,β2一般取0.99,ε一般取1e-10。
2.4 Learning Rate Scheduling
- 学习率衰减(Learning Rate Decay)——为了防止学习率过大,在收敛到全局最优点的时候会来回摆荡,所以要让学习率随着训练轮数不断下降,收敛梯度下降的学习步长。其中包括线性衰减(例如:每过5个epochs学习率减半)、指数衰减(随着迭代轮数的增加学习率自动发生衰减)、分段常数衰减等方法。
- 热启动(Warm up)——warmup是初始阶段使用较小学习率启动,后期恢复正常;而decay是初始时使用较大的学习率,之后进行衰减。其有助于减缓模型在初始阶段对mini-batch的提前过拟合现象,保持分布的平稳。
4 损失函数(Loss)的影响
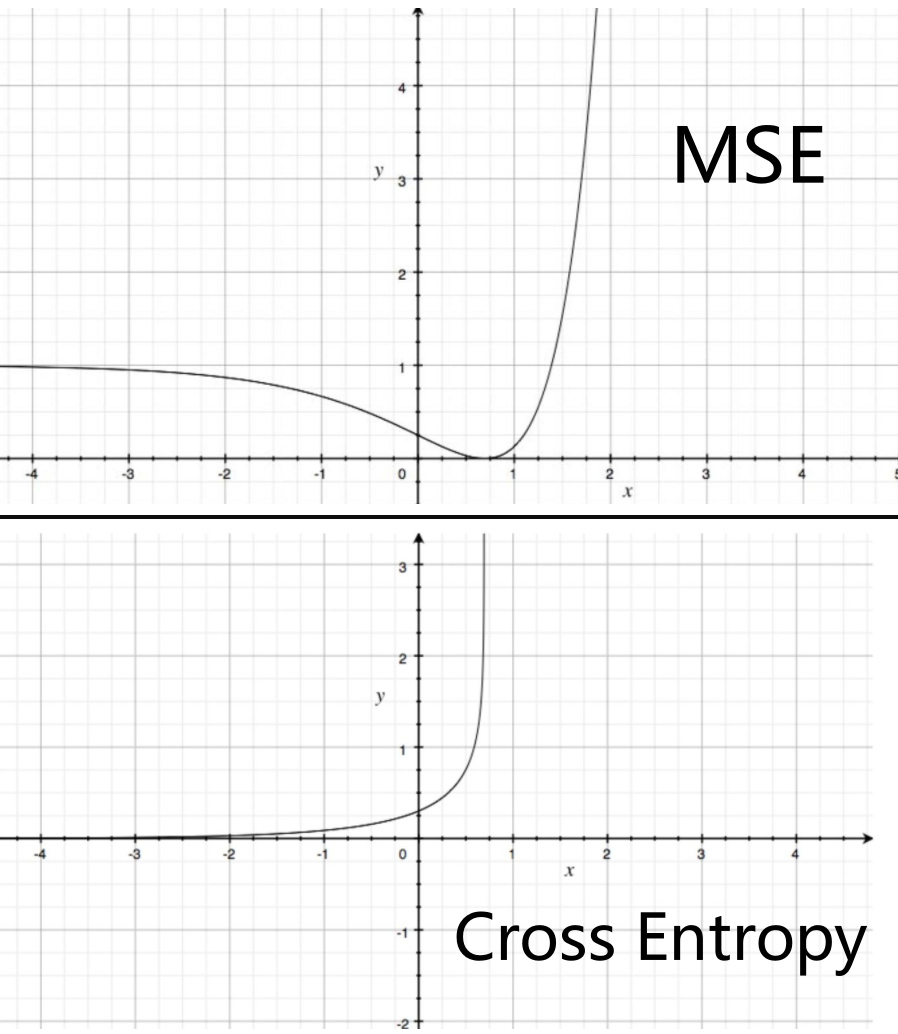
均方误差(Mean Square Error,MSE)适用于回归问题,而交叉熵(Cross Entropy)适用于分类问题。
在分类问题中,MSE损失函数为$\text { loss }=\frac{1}{2 m} \sum_{i}^{m}\left(y_{i}-y^{\prime}\right)^{2}$,加上softmax之后为$\operatorname{los} s_{i}=\left(c_{1}-\frac{e^{y i^{\prime}}}{c_{2}}\right)^{2}$,是一个非凸函数,梯度下降算法难以达到全局最优解。所以MSE在分类问题中,并不是一个好的loss函数;而交叉熵损失函数为$\operatorname{loss}=-\sum_{i=1}^{n} y_{i} * \log \left(y_{i}\right)$,加入softmax得到$\operatorname{loss}{i}=-\log \left(c{1}-\frac{e^{x}}{c_{2}}\right)$。
相对MSE而言,交叉熵曲线整体呈单调性,loss越大,梯度越大。便于梯度下降反向传播,利于优化。所以一般针对分类问题采用交叉熵作为loss函数。(P.S.在广义伯努利分布下,最小化交叉熵损失等同于极大似然估计)
5 批量标准化/归一化(Batch Normalization,BN)
Batch Normalization,简称BatchNorm或BN,翻译为“批归一化”,是神经网络中一种特殊的层,如今已是各种流行网络的标配。在原始论文中,BN被建议插入在(每个)ReLU激活层前面。
BN操作分为两步:
- Standardization:首先对$m$个$x$进行Standardization,得到zero mean unit variance的分布$\hat{x}$。
- scale and shift:然后再对$\hat{x}$进行scale and shift,缩放并变换回原始的分布$y$。(这样的目的是为了补偿网络的非线性表达能力,因为经过标准化之后,偏移量丢失。均值$\beta$方差$\gamma$相当于输入数据分布的方差和偏移。)
Batch Normalization有以下几点优势:
- BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度
- BN使得模型对网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定
- BN允许网络使用饱和性激活函数(例如sigmoid,tanh等),缓解梯度消失问题
- BN具有一定的正则化效果