李宏毅机器学习——反向传播

1 反向传播原理

神经网络中求解权重W的算法，分为信号的前向传播（Forward propagation，FP）和反向传播（Back propagation，BP）。前向传播得到预测值，计算输出误差，然后计算每个神经元节点对误差的贡献；反向传播根据前向传播的误差来求梯度，然后根据贡献调整原来的权重，最终达到最小化损失函数的目的。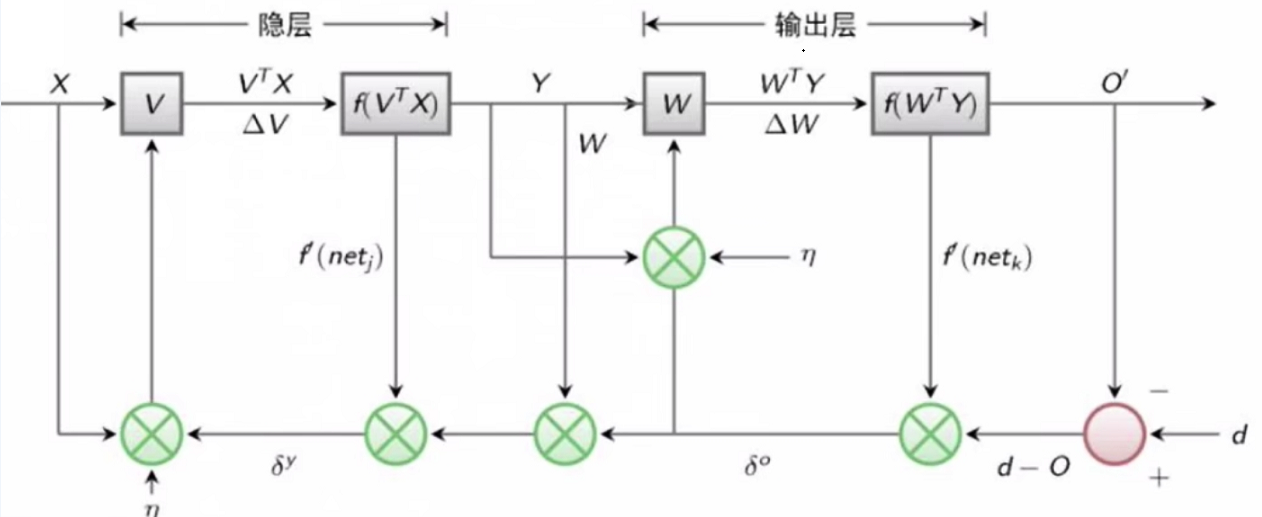

假设只有一个隐含层，设L为损失函数。
在输出层上的误差（这里$O_{k}$就是输出值$y_{out}$。）：
$$
L_{total}=\frac{1}{2}(d-O)^{2}=\frac{1}{2} \sum_{k=1}^{\ell}\left(d_{k}-O_{k}\right)^{2}
$$

在隐含层上的误差（这里$net_{k}=\sum(w_i*O_{k})+b$。）：
$$
L_{total}=\frac{1}{2} \sum_{k=1}^{c}(d_{k}-f[\sum_{j=0}^{m} w_{j k} f(n e t_{j})])^{2}=\frac{1}{2} \sum_{k=1}^{c}(d_{k}-f[\sum_{j=0}^{m} w_{j k} f(\sum_{i=1}^{n} v_{i j} x_{i}))^{2}
$$

在输入层上的误差：
$$
L_{total}=\frac{1}{2} \sum_{k=1}^{c}\left(d_{k}-f\left[\sum_{j=0}^{m} w_{j k} f\left(n e t_{j}\right)\right]\right)^{2}=\frac{1}{2} \sum_{k=1}^{c}\left(d_{k}-f\left[\sum_{j=0}^{m} w_{j k} f\left(\sum_{i=1}^{n} v_{i j} x_{i}\right)\right]\right)^{2}
$$

用误差L对每一个权重$w$求偏导（链式法则），就是代表该权重$w$对总体误差产生了多少影响。
$$
w_{i}^{+}=w_{i}-\eta * \frac{\partial L_{\text {total }}}{\partial w_{i}}
$$
用同样的方法更新所有权重$w$，最后不停地迭代使误差降低。

2 numpy实现反向传播

import numpy as np

def scaling(data):	#数据归一化
    max = np.max(data,0)
    min = np.min(data,0)
    return (data-min)/(max-min)

def sigmoid(data):	#激活函数
    return 1/(1+np.exp(-data))

def wb_calc(X,y,alpha=0.1,maxIter=10000,n_hidden_dim=3,reg_lamda=0):
	#FP
	#初始化
    W1 = np.mat(np.random.randn(2,n_hidden_dim))
    b1 = np.mat(np.random.randn(1,n_hidden_dim))
    W2 = np.mat(np.random.randn(n_hidden_dim,1))
    b2 = np.mat(np.random.randn(1,1))
    for stepi in range(maxIter):
        z1 = x*W1 + b1
        a1 = sigmoid(z1)
        z2 = a1*W2 + b2
        a2 = sigmoid(z2)
    
    #BP
    	#初始化
        a0 = X.copy()
		deltal2 = a2 - ymat
        deltal1 = np.mat((deltal2*W2.T).A * a1.A(1-a1).A)	#.A表示转化为数组
    	dW1 = a0.T+deltal1 + reg_lambda*W1
        db1 = np.sum(deltal1,0)
        dW2 = a1.T+deltal2 + reg_lambda*W2
        db2 = np.sum(deltal2,0)
        #更新w,b
        W1 = W1 - alpha*dW1
        b1 = b1 - alpha*db1
        W2 = W2 - alpha*dW2
        b2 = b2 - alpha*db2

    return W1,b1,W2,b2

参考资料

1.b站李宏毅《机器学习》
2.datawhale李宏毅机器学习笔记(LeeML-Notes)