李宏毅机器学习——梯度下降
1 偏差与方差
使用样本数据拟合函数,由于样本数据使采样而并非真实值本身,采样本身会带来误差。经过研究发现,其误差的期望值可以分解为三个部分:样本噪音、模型预测值的方差、预测值相对真实值的偏差,公式为:
$$
E\left((y-\hat{f}(x))^{2}\right)=\sigma^{2}+\operatorname{Var}[\hat{f}(x)]+(\operatorname{Bias}[\hat{f}(x)])^{2}
$$
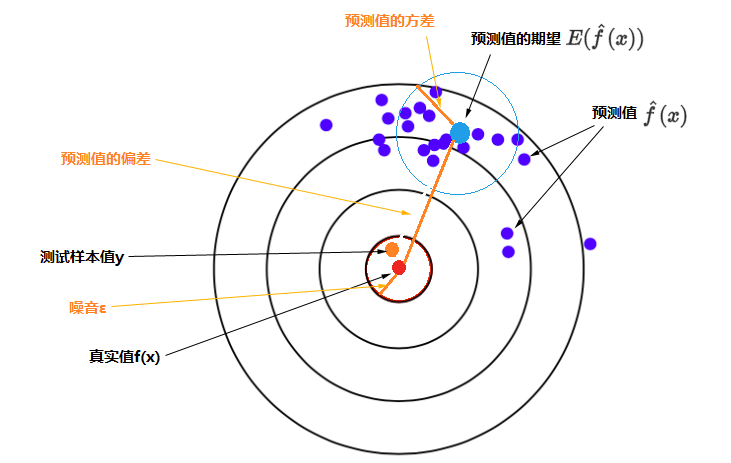
其中$Bias[\hat{f}(x)] = E[\hat{f}(x) - f(x)]$,即误差的期望值 = 噪音的方差 + 模型预测值的方差 + 预测值相对真实值的偏差的平方,如下图所示。
靶心(红点)是测试样本的真实值,测试样本的y(橙色点)是真实值加上噪音,特定模型重复多次训练会得到多个具体的模型,每一个具体模型对测试样本进行一次预测,就在靶上打出一个预测值(图上蓝色的点)。所有预测值的平均就是预测值的期望(较大的浅蓝色点),浅蓝色的圆圈表示预测值的离散程度,即预测值的方差。
2 调整梯度下降的学习率
如果每次调的太大,loss变化就很快:调的太小,loss变化的太慢,这样都找不到最小的loss。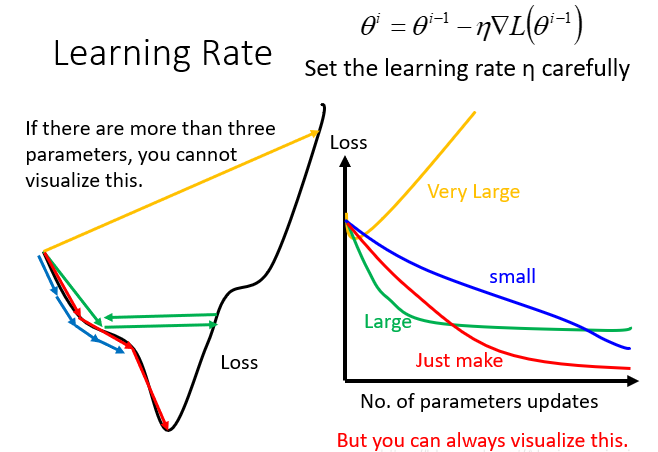
此时我们可以采用自适应学习率,即刚开始时,初始点距离最低点较远,采用较大的学习率,在每次更新参数后,更接近最低点了,调小学习率。于是就有了不同的优化梯度下降的方法,这类优化梯度下降的方法有SGD、AdaGrad、Adam等等。
2.1 SGD
批量梯度下降(Batch Gradient Descent,BGD)是在全部训练集上计算准确的梯度,即
$$
\sum_{i=1}^{n} \nabla_{\theta} f\left(\theta ; x_{i}, y_{i}\right)+\nabla_{\theta} \phi(\theta)
$$
而随机梯度下降(Stochastic Gradient Descent,SGD)则是采样单个样本来估计当前的梯度,即
$$
\nabla_{\theta} f\left(\theta ; x_{i}, y_{i}\right)+\nabla_{\theta} \phi(\theta)
$$
SGD最大的缺点是下降速度慢和不稳定,而且可能会在沟壑的两边持续震荡,停留在一个局部最优点。
2.2 SGD with Momentum
为了抑制SGD的震荡,SGDM认为梯度下降过程可以加入惯性。下坡的时候,如果发现是陡坡,那就利用惯性跑的快一些。SGDM在SGD基础上引入了一阶动量:
$$
m_{t}=\beta_{1} \cdot m_{t-1}+\left(1-\beta_{1}\right) \cdot g_{t}
$$
一阶动量是各个时刻梯度方向的指数移动平均值,约等于最近$1 /\left(1-\beta_{1}\right)$个时刻的梯度向量和的平均值。也就是说,t时刻的下降方向,不仅由当前点的梯度方向决定,而且由此前累积的下降方向决定。这就意味着下降方向主要是此前累积的下降方向,并略微偏向当前时刻的下降方向。
2.3 SGD with Nesterov Acceleration
SGD 还有一个问题是困在局部最优的沟壑里面震荡。因此,我们不能停留在当前位置去观察未来的方向,而要向前一步、多看一步、看远一些。
NAG全称Nesterov Accelerated Gradient,是在SGD、SGD-M的基础上的进一步改进。NAG不计算当前位置的梯度方向,而是计算如果按照累积动量走了一步,那个时候的下降方向:
$$
g_{t}=\nabla f\left(w_{t}-\alpha \cdot m_{t-1} / \sqrt{V_{t-1}}\right)
$$
2.5 Adgrad
Adagrad是解决不同参数应该使用不同的更新速率的问题。Adagrad自适应地为各个参数分配不同学习率的算法。
其公式如下: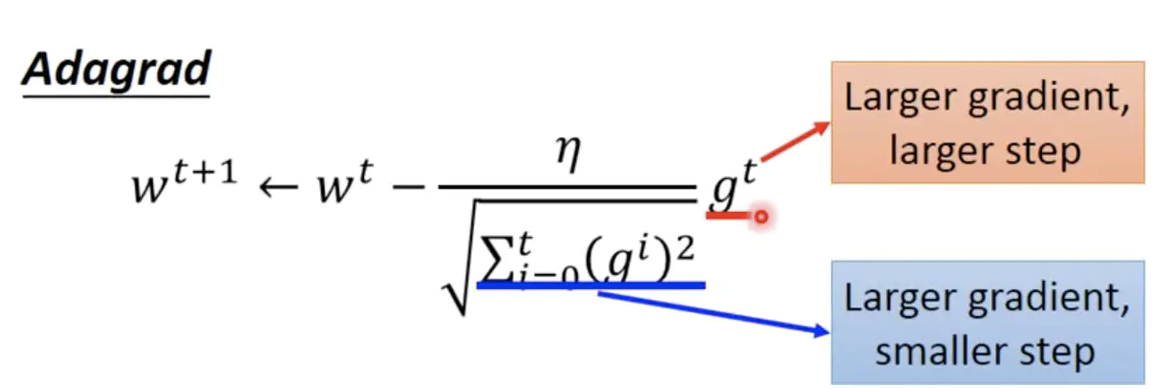
Adagrad设置全局学习率之后,每次通过全局学习率逐参数的除以历史梯度平方和的平方根,使得每个参数的学习率不同。这里的梯度平方和就是二阶动量。
Adagrad起到的效果是在参数空间更为平缓的方向会取得更大的进步(因为平缓,所以历史梯度平方和较小,对应学习下降的幅度较小),并且能够使得陡峭的方向变得平缓,从而加快训练速度。
Adagrad的缺点是由于是累积平方梯度,平方梯度是单调递增函数,会使得学习率单调递减至0,从而使训练过程提前结束。
2.6 AdaDelta / RMSProp
由于AdaGrad单调递减的学习率变化过于激进,可以改进二阶动量计算方法:不累积全部历史梯度,而只关注过去一段时间窗口的下降梯度。(这也是AdaDelta名称中Delta的来历。)
指数移动平均值大约就是过去一段时间的平均值,因此可以用这一方法来计算二阶累积动量:
$$
V_{t}=\beta_{2} * V_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2}
$$
这可以避免二阶动量持续累积、导致训练过程提前结束的问题。
2.7 Adam
SGD-M在SGD基础上增加了一阶动量,AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来,就是Adam了——Adaptive + Momentum。
SGD的一阶动量:
$$
m_{t}=\beta_{1} \cdot m_{t-1}+\left(1-\beta_{1}\right) \cdot g_{t}
$$
加上AdaDelta的二阶动量:
$$
V_{t}=\beta_{2} * V_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2}
$$
其中$\beta_{1}$控制一阶动量,$\beta_{2}$控制二阶动量。
2.8 Nadam
在Adam的基础上增加了Nesterov,即同时用上一二阶动量,且按照累积动量走了一步。
$$
g_{t}=\nabla f\left(w_{t}-\alpha \cdot m_{t-1} / \sqrt{V_{t}}\right)
$$
3 特征缩放(Feature Scaling)
特征缩放(Feature Scaling)包括标准化(Standardization/Z-Score Normalization)和归一化(Normalization)。特征缩放可以同一量纲和数量级,可以提高某些基于距离的算法(Distance-Based Algorithms),如KNN、K-Means、SVM、PCA等距离计算算法的性能,但对基于树的算法(Tree-Based Algorithms)、线性判别分析、朴素贝叶斯等算法无帮助。
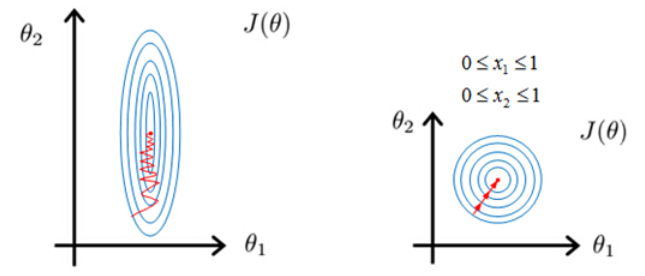
特征缩放对于基于梯度下降的算法(Gradient Descent Based Algorithms)有加速作用——未经标准化的特征的损失函数是椭圆形,梯度下降方向垂直于等高线,形成zigzag的路线,并非指向local mininum。对特征进行归一化Normalization后,其损失函数的等高线图更接近圆形,梯度下降的方向震荡更小,收敛更快。