李宏毅机器学习——回归
回归大致可以理解为根据数据集$D$,拟合出近似的曲线,所以回归也常称为拟合(Fit)。按照自变量的数量可以分为一元回归和多元回归,按照自变量与因变量之间的函数表达式可以分为线性回归(Linear Regression)和非线性回归(Non-linear Regression)。
1 模型步骤
- Step1:模型假设,选择模型框架(线性模型)
- Step2:模型评估,如何判断众多模型的好坏(损失函数)
- Step3:模型优化,如何筛选最优的模型(梯度下降)
1.1 模型假设(多元线性模型)
多元线性模型就是特征x的线性组合的函数,可以表示为$y=\sum{w_ix_i}+b$,$x_i$为特征,$w_i$为权重,b为偏移量。
1.2 模型评估(损失函数)
常用的损失函数是均方误差(mean-square error, MSE),也被称为最小二乘法 (least square method),其几何意义就是欧氏距离。
不同的loss函数,具有不同的拟合特性:
Hinge Loss——SVM;
exp-Loss ——Boosting;
log-Loss——Logistic Regression。
Square loss损失函数表示为:
$$
L\left( w,b \right) =\sum_{i=1}^m{\left( f\left( x_i \right) -y_i \right) ^2},
$$
我们需要找到令结果最小的$w^*$和$b^*$,即
$$
\left( w^*,b^* \right) =arg\min {\left( w,b \right)}\sum{i=1}^m{\left( f\left( x_i \right) -y_i \right) ^2}。
$$
1.3 最佳模型(解析解)
多元(多个特征)的情况下,损失函数可以引入矩阵表示为:
$$
L\left( w,b \right) =\sum_{i=1}^m{\left( f\left( x_i \right) -y_i \right) ^2}=\left( XW-y \right) ^T\left( XW-y \right)
$$
式中,$X$是一组样本形成的样本矩阵,$W$是权重矩阵,$y$是样本真实值形成的矩阵。
上式可以展开为:
$$
L\left( w,b \right) =\left( XW-y \right) ^T\left( XW+y \right)
$$
$$
=\left( \left( XW \right) ^T-y^T \right) \left( XW-y \right)
$$
$$
=\left( X^TW^T-y^T \right) \left( XW-y \right)
$$
$$
=X^TW^TXW-y^TXW-W^TX^Ty+y^Ty
$$
对$w$求导:
$$
\frac{\partial L\left( W \right)}{\partial W}=2X^TXW-\left( y^TX \right) ^T-X^Ty
$$
$$
=2X^TXW-2X^Ty
$$
偏导等于零时可以求得损失函数最小时对应的$W$,即我们最终想要获得的系数矩阵:
$$
X^TXW-X^Ty=0
$$
$$
X^TXW=X^Ty
$$
$$
((X^TX)^{-1}X^TX)W=(X^TX)^{-1}X^Ty
$$
$$
IW=(X^TX)^{-1}X^Ty
$$
$$
W=(X^TX)^{-1}X^Ty
$$
上式必须满足矩阵的逆存在,而矩阵可逆需要方正且满秩。但是因为不能保证所选的特征是完全线性无关的,所以矩阵不一定满秩,这导致线性回归有解析解但存在无穷多解,还是无法求得一个准确的解,这时候就需要使用梯度下降法来逼近一个解。
1.4 最佳模型(梯度下降法)
首先设置初始的$w_0$和$b_0$,然后通过求$L$对$w$和$b$的偏导不断地更新$w$和$b$,直到找到$L$的最小值。
整个过程可以表示为:
$$
repeat,,until,,converge{w_i:=w_i-\eta \frac{\partial L\left( w_i \right)}{w_i};\ b_i:=b_i-\eta \frac{\partial L\left( b_i \right)}{b_i}}
$$
其中$\eta $是学习率,用来控制每步下降的距离(太小收敛会很慢,太大则可能跳过最优点),一般按照对数的方法来选择,例如0.1, 0.03, 0.01, 0.003…这种方法称为批量梯度下降(batch gradient descent, BGD)
original-loss存在很多奇点,而BGD每次下降的方向就是original-loss的负梯度,因此BGD很容易陷入某个奇点,而无法达到global minimal(或者比较好的local minimal)。随机梯度下降(stochastic gradient descent, SGD)一定程度上可以避免这个情况——不容易陷入original-loss和minibatch-loss的奇点:
- 引入randomness,SGD中计算的梯度是对original-loss梯度的近似,相当于在original-loss梯度的基础上加了randomness,因此即使当前走到了original-loss的奇点,SGD计算的梯度因为引入了randomness,所以也不接近0,比较容易跳出奇点。
- SGD计算的不是original-loss的梯度,而是minibatch-loss的梯度,original-loss和minibatch-loss的形状不同,奇点分布也不同,如果当前这个点在original-loss上是奇点,但这个点在minibatch-loss中并不是奇点,此时使用minibatch-loss的负梯度作为下降方向,自然不会陷入这个点。
- 每次迭代,都会使用不同的mini batch,而不同的minibatch-loss的形状不同。就算此时陷入了当前minibatch-loss的奇点,那么下一次迭代,这个点也不一定就是下一个minibatch-loss的奇点,如果不是的话,自然就跳出来了。
1.5 正则化
当我们筛选出模型进行拟合数据时,可能会没有很好地拟合数据,称为欠拟合(underfitting),或者叫做高偏差(bias);也可能对训练集拟合得很好,但在测试集上拟合不好,称为过拟合(overfitting),也叫高方差(variance)。
对于过拟合,我们可以
- 1.减少选取变量的数量(通过特征选择保留更为重要的特征变量)
特征选择的缺点在于:舍弃一部分特征变量的同时,也舍弃了问题中的一些信息。
如果我们不想舍弃这些信息,可以使用正则化。
- 2.正则化
当线性回归从1次变成高次的过程中,在训练集上的拟合越来越好,但在测试集上并不是这样。于是我们可以采用正则化,去惩罚$w_1$到$w_n$,以L2正则化为例,原始的损失函数$L$上加上$\lambda \sum{\left( w_i \right) ^2}$,使得权重的绝对值大小整体倾向于减小(权重衰减),这样可以使函数更加平滑,也就是更加简单,不容易发生过拟合。形象一点看,损失函数曲面通过L2正则化的加持,最小值所在的位置从一条山岭变成一个山谷,故L2正则化在机器学习中也叫做“岭回归”(ridge regression)。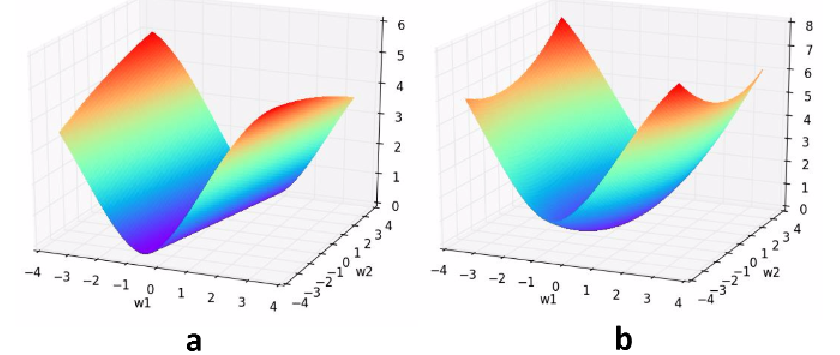
L1正则化则是加上$\lambda \sum{\left| \left. w_i \right| \right.}$,L1 正则化除了和L2正则化一样可以约束数量级外,还能使参数更加稀疏,参数一部分为0,另一部分为非零实值。非零实值的那部分参数值可起到选择重要参数或特征维度的作用,同时可起到去除噪声的效果。
2 sklearn实现多元线性回归
1 | import pandas as pd |
