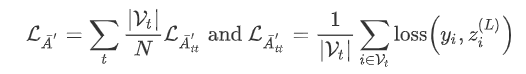图神经网络——超大图上的节点表征学习

Posted on | In |
Words count in article: 2.4k

图卷积网络(GCN)已经成功地应用于许多基于图形的应用，然而大规模的GCN的训练仍然具有挑战性。目前基于SGD的算法要么面临着随GCN层数呈指数增长的高计算成本，要么面临着保存整个图形和每个节点的embedding到内存的巨大空间(显存)需求。于是论文Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Network提出了Cluster-GCN方法来解决超大图的训练问题。

1.Cluster-GCN方法简单概括

  • 利用图节点聚类算法将一个图的节点划分为$c$个簇，每一次选择几个簇的节点和这些节点对应的边构成一个子图，然后对子图做训练。
  • 由于是利用图节点聚类算法将节点划分为多个簇，所以簇内边的数量要比簇间边的数量多得多，所以可以提高表征利用率，并提高图神经网络的训练效率。
  • 每一次随机选择多个簇来组成一个batch，这样不会丢失簇间的边，同时也不会有batch内类别分布偏差过大的问题。
  • 基于小图进行训练，不会消耗很多内存空间，于是我们可以训练更深的神经网络，进而可以达到更高的精度。

2.GCN回顾

论文2017. Semi-supervised classification with graph convolutional networks中提出了GCN。作者定义了一种类似卷积的运算，称为谱图卷积。这使得CNN可以直接在图形上操作。GCN中的每一层通过考虑相邻节点的embedding，来更新Graph中的每个节点的特征向量表示。GCN的逐层正向传播可以总结为：
$$
X^{\left( l+1 \right)}=f\left( X^l,A \right) =\sigma \left( \tilde{D}^{-\frac{1}{2}}\tilde{A}D^{-\frac{1}{2}}X^{\left( l \right)}W^{\left( l \right)} \right)
$$

  • $X$是所有节点的特征向量构成的特征矩阵。
  • $X^l$和$X^{l+1}$分别是$l$层的输入和输出矩阵，$X^l$也是第$l$层对于所有节点的embedding。
  • A是图的邻接矩阵。
  • ${A}=A+I_N$是带有自环的无向图的邻接矩阵。
  • $I_N$是单位矩阵。
  • $\tilde{D}{ii}=\sum{\tilde{A}{ij}}$是带有自环的无向图的度矩阵，是一个对角矩阵。
  • $W^{(l)}$是一个可训练权重矩阵或参数矩阵。
  • $\sigma(\cdot)$是激活函数，通常被设为ReLU。

为了简化计算，假设所有层的表征维度都是F，上式写为：
$$
Z^{(l+1)}=A^{\prime} X^{(l)} W^{(l)}, X^{(l+1)}=\sigma\left(Z^{(l+1)}\right)
$$

  • $A^{\prime}$是归一化和规范化后的邻接矩阵

将GCN用于半监督节点分类时，目标是通过最小化损失函数来学习上式中的权重矩阵：
$$
\mathcal{L}=\frac{1}{\left|\mathcal{Y}{L}\right|} \sum{i \in \mathcal{Y}{L}} \operatorname{loss}\left(y{i}, z_{i}^{L}\right)
$$

  • $\mathcal{Y}_{\mathcal{L}}$是节点类别。
  • $z_{i}^{(L)}$是$Z^{(L)}$的第$i$行，表示节点$i$的最终层预测。
  • $y_{i}$为节点$i$的真实类别。

    3.Cluster-GCN的速度

    原始的GCN的训练使用的是全批量梯度下降(Full Gradient Descent)，它的计算和内存成本很高:
  • 在内存方面，通过反向传播来计算full gradient需要存储所有的embedding矩阵，这需要O(NFL)的内存空间（F是特征数量，N是结点数量，L是网络层数）。
  • 在收敛速度方面，由于在每个epoch模型才更新一次，所以需要很多个epoch才会使模型达到收敛。

mini-batch SGD可以提高GCN的训练速度，其不需要计算整个梯度，只需要计算每次更新的mini-batch的梯度。使用大小为$b=|\mathcal{B}|$的$\mathcal{B} \subseteq[N]$来表示一个batch的节点索引。SGD的每一步都将计算梯度估计值$\frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \nabla \operatorname{loss}\left(y_{i}, z_{i}^{(L)}\right)$来进行参数更新。

尽管在每个epoch收敛得更快，但SGD在GCN训练上引入了另一个计算开销（邻域扩展），这使得SGD的每个epoch时间内比全梯度下降（full gradient descent）要慢得多——计算一个节点$i$的梯度，需要节点$i$的embedding，而节点$i$的embedding的依赖于前面的层里的它的邻居的embeddings，为了提取前面的层中它的邻居节点embeddings，还需要进一步聚合每个邻居节点的邻居节点的embeddings。假设一个图神经网络有$L+1$层，节点的平均的度为$d$。为了得到节点$i$的梯度，需要聚合图上$O\left(d^{L}\right)$的节点的表征，与权重矩阵$W^{(l)}$相乘，所以计算任意节点表征的时间开销是$O\left(F^{2}\right)$。所以SGD一个节点的梯度的计算需要$O\left(d^{L} F^{2}\right)$的时间。

4.Cluster-GCN详解

在mini-batch SGD更新中，设计一个batch和相应的计算sub graph来最大限度地提高embedding utilization。Cluster-GCN通过将embedding utilization连接到一个聚类目标上来实现。

对于一个Graph$G$，我们将其节点划分为$c$个簇：$\mathcal{V}=\left[\mathcal{V}{1}, \cdots \mathcal{V}{c}\right]$，其中$\mathcal{V}{t}$由第$t$个簇中的节点组成，得到$c$个子图:
$$
\bar{G}=\left[G{1}, \cdots, G_{c}\right]=\left[\left{\mathcal{V}{1}, \mathcal{E}{1}\right}, \cdots,\left{\mathcal{V}{c}, \mathcal{E}{c}\right}\right]
\notag
$$
其中$\mathcal{E}{t}$只由$\mathcal{V}{t}$中的节点之间的边组成。经过节点重组，邻接矩阵被划分为大小为$c^{2}$的块矩阵，如下所示
$$
A=\bar{A}+\Delta=\left[\begin{array}{ccc}
A_{11} & \cdots & A_{1 c} \
\vdots & \ddots & \vdots \
A_{c 1} & \cdots & A_{c c}
\end{array}\right]
$$
其中
$$
\bar{A}=\left[\begin{array}{ccc}
A_{11} & \cdots & 0 \
\vdots & \ddots & \vdots \
0 & \cdots & A_{c c}
\end{array}\right], \Delta=\left[\begin{array}{ccc}
0 & \cdots & A_{1 c} \
\vdots & \ddots & \vdots \
A_{c 1} & \cdots & 0
\end{array}\right]
$$

  • 对角线上的块$A_{t t}$是大小为$\left|\mathcal{V}{t}\right| \times\left|\mathcal{V}{t}\right|$的邻接矩阵，它由$G_{t}$内部的边构成。
  • $\bar{A}$是图$\bar{G}$的邻接矩阵。
  • $A_{s t}$由两个簇$\mathcal{V}{s}$和$\mathcal{V}{t}$之间的边构成。
  • $\Delta$是由$A$的所有非对角线块组成的矩阵。

用块对角线邻接矩阵$\bar{A}$去近似邻接矩阵$A$之后，完整的损失函数可以根据batch分解成多个部分之和：

W2fREV.png

W2fX4O.png

Cluster-GCN使用了Graph聚类算法来划分Graph。Graph聚类的方法，如metis和graclus等，旨在在Graph中的顶点上构建分区，使得簇内连接远大于簇间连接，从而更好的捕捉聚类和区分结构。

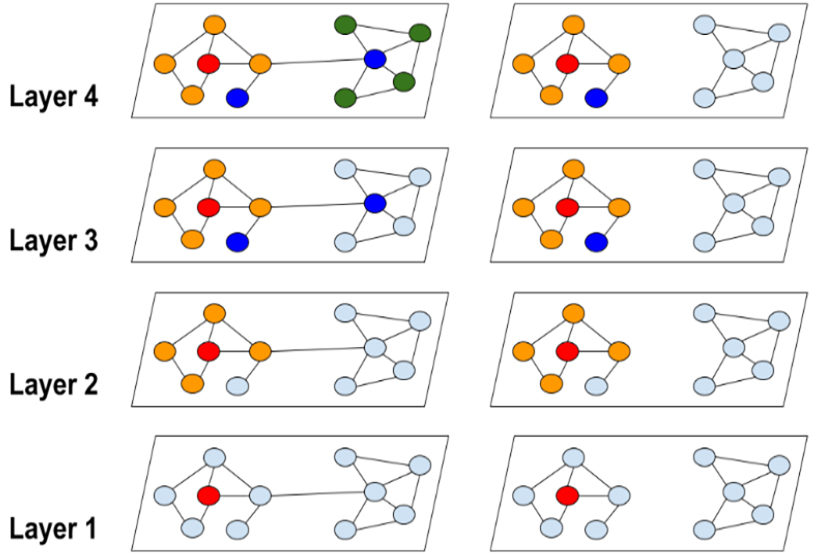
LAYER.jpg

5.Cluster-GCN实践

PyG库中提供了Cluster-GCN的接口，可以像训练普通神经网络一样在超大图上训练图神经网络。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#导入库和数据集
import torch
import torch.nn.functional as F
from torch.nn import ModuleList
from torch_geometric.nn import SAGEConv
from tqdm import tqdm
from torch_geometric.datasets import Reddit, Reddit2
from torch_geometric.data import ClusterData, ClusterLoader, NeighborSampler

dataset = Reddit('../dataset/Reddit')
data = dataset[0]
print(dataset.num_classes)
print(data.num_nodes)
print(data.num_edges)
print(data.num_features)

结果：
41, 232965, 114615892, 602

1
2
3
4
5
6
#图节点聚类并生成数据加载器
cluster_data = ClusterData(data, num_parts=1500, recursive=False, save_dir=dataset.processed_dir)

train_loader = ClusterLoader(cluster_data, batch_size=20, shuffle=True, num_workers=12)

subgraph_loader = NeighborSampler(data.edge_index, sizes=[-1], batch_size=1024, shuffle=False,num_workers=12)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#构建网络
class Net(torch.nn.Module):
    def __init__(self, in_channels, out_channels):
        super(Net, self).__init__()
        self.convs = ModuleList(
            [SAGEConv(in_channels, 128),
             SAGEConv(128, out_channels)])

    def forward(self, x, edge_index):
        for i, conv in enumerate(self.convs):
            x = conv(x, edge_index)
            if i != len(self.convs) - 1:
                x = F.relu(x)
                x = F.dropout(x, p=0.5, training=self.training)
        return F.log_softmax(x, dim=-1)

    def inference(self, x_all):
        pbar = tqdm(total=x_all.size(0) * len(self.convs))
        pbar.set_description('Evaluating')
        
        for i, conv in enumerate(self.convs):
            xs = []
            for batch_size, n_id, adj in subgraph_loader:
                edge_index, _, size = adj.to(device)
                x = x_all[n_id].to(device)
                x_target = x[:size[1]]
                x = conv((x, x_target), edge_index)
                if i != len(self.convs) - 1:
                    x = F.relu(x)
                xs.append(x.cpu())

                pbar.update(batch_size)

            x_all = torch.cat(xs, dim=0)

        pbar.close()

        return x_all

此神经网络的forward函数的定义与普通的图神经网络并无区别，而inference方法应用于推理阶段，为了获取更高的预测精度，所以使用subgraph_loader。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#训练、验证、测试
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net(dataset.num_features, dataset.num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)

def train():
    model.train()

    total_loss = total_nodes = 0
    for batch in train_loader:
        batch = batch.to(device)
        optimizer.zero_grad()
        out = model(batch.x, batch.edge_index)
        loss = F.nll_loss(out[batch.train_mask], batch.y[batch.train_mask])
        loss.backward()
        optimizer.step()

        nodes = batch.train_mask.sum().item()
        total_loss += loss.item() * nodes
        total_nodes += nodes

    return total_loss / total_nodes

@torch.no_grad()
def test():  # Inference should be performed on the full graph.
    model.eval()

    out = model.inference(data.x)
    y_pred = out.argmax(dim=-1)

    accs = []
    for mask in [data.train_mask, data.val_mask, data.test_mask]:
        correct = y_pred[mask].eq(data.y[mask]).sum().item()
        accs.append(correct / mask.sum().item())
    return accs

for epoch in range(1, 31):
    loss = train()
    if epoch % 10 == 0:
        train_acc, val_acc, test_acc = test()
        print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}, Train: {train_acc:.4f}, '
              f'Val: {val_acc:.4f}, test: {test_acc:.4f}')
    else:
        print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}')

结果：
Epoch: 10, Loss: 0.2893, Train: 0.9620, Val: 0.9516, test: 0.9496
Epoch: 20, Loss: 0.2478, Train: 0.9664, Val: 0.9546, test: 0.9560
Epoch: 30, Loss: 0.2397, Train: 0.9689, Val: 0.9515, test: 0.9502

在训练过程中，使用train_loader获取batch，每次根据多个簇组成的batch进行训练；在验证阶段，使用subgraph_loader，在计算一个节点的表征时会计算该节点的距离从$0$到$L$的邻接节点，可以更好地测试神经网络的性能。

参考资料

1.datawhale-GNN开源学习资料
2.Cluster-GCN论文

欢迎关注我们的公众号
0%