图神经网络——基本图论与PyG库

Posted on | In |
Words count in article: 2.1k

在以往的深度学习中，主要的数据形式包括矩阵、张量、序列(sequence)和时间序列(time series)，然而还有许多数据是图的结构，如社交网络、知识图谱等。图结构数据具有以下特点：

任意的大小和复杂的拓扑结构；
没有固定的节点排序或参考点；
通常是动态的，并具有多模态的特征；
图的信息包括节点信息、边信息和拓扑结构信息。

1. 图结构数据

1.1 图(Graphs)

· 一个图记作$\mathcal{G}={\mathcal{V}, \mathcal{E}}$，其中 $\mathcal{V}=\left{v_{1}, \ldots, v_{N}\right}$是数量为$N=|\mathcal{V}|$ 的节点的集合， $\mathcal{E}=\left{e_{1}, \ldots, e_{M}\right}$ 是数量为 $M$ 的边的集合。
· 节点表示实体(entities)，边表示实体间的关系(relations)；节点和边的信息可以是类别型或数值型的。
· 只有一种类型的节点和一种类型的边的图称为同质图(Homogeneous Graph)。
· 存在多种类型的节点和多种类型的边的图称为异质图(Heterogeneous Graph)

1.2 图的邻接矩阵(Adjacency Matrix)

· 图$\mathcal{G}={\mathcal{V}, \mathcal{E}}$，其对应的邻接矩阵记为$\mathbf{A} \in{0,1}^{N \times N}$。$\mathbf{A}{i, j}=1$表示存在从节点$v_i$到$v_j$的边，反之表示不存在从节点$v_i$到$v_j$的边。
· 在无向图中，节点$v_i$到$v_j$的边存在，则节点$v_j$到$v_i$的边也存在，所以无向图的邻接矩阵的对称的。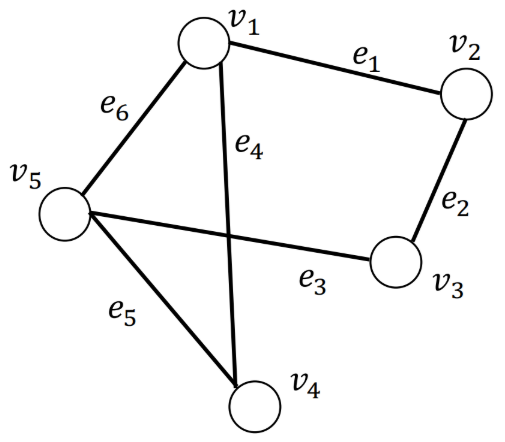
图1
其邻接矩阵为：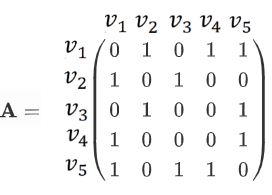
图2
· 在无权图中，各条边的权重是等价的，都为1。
· 在有权图中，其对应的邻接矩阵通常被记为$\mathbf{W} \in{0,1}^{N \times N}$，其中$\mathbf{W}{i, j}=w_{ij}$表示从节点$v_i$到$v_j$的边的权重。若边不存在时，边的权重为$0$。

1.3 节点的度(degree)

· 在有向有权图中，节点$v_i$的出度(out degree)等于从$v_i$出发的边的权重之和，节点$v_i$的入度(in degree)等于从连向$v_i$的边的权重之和；节点$v_i$的度记为$d(v_i)$，入度记为$d_{in}(v_i)$，出度记为$d_{out}(v_i)$。
· 在无向图中，出度=入度。
· 在无权图中，入读等于连向$v_i$的边的数量，出度等于从$v_i$出发的边的数量。

1.4 邻接节点(neighbors)

· 与节点$v_i$直接相连的节点称为邻接节点，记为**$\mathcal{N(v_i)}$**。
· 与节点$v_i$距离$k$步的称为$k$跳远的邻接节点(neighbors with $k$-hop) [一个节点的$2$跳远的邻接节点包含自身]

1.5 行走(walk)

· $walk(v_1, v_2) = (v_1, e_6,e_5,e_4,e_1,v_2)$，这是一次“行走”，从节点$v_1$出发，依次经过边$e_6,e_5,e_4,e_1$，最终到达节点$v_2$的“行走”。
· “行走”中，节点允许重复。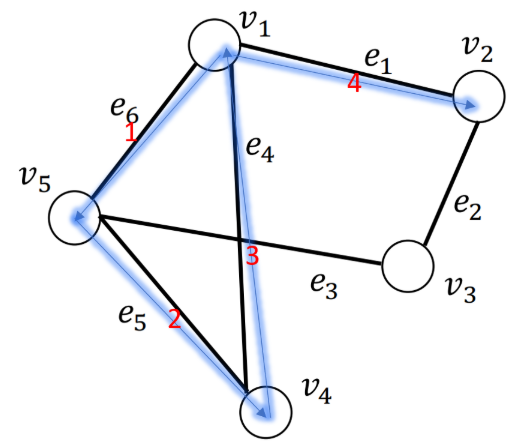
图3

1.6 路径(path)

“路径”是节点不可重复的“行走”。

1.7 子图(subgraph)

指节点集和边集分别是整图的节点集的子集和边集的子集的图。

1.8 连通分量(connected component)

图$\mathcal{G}={\mathcal{V}, \mathcal{E}}$的子图为$\mathcal{G}^{\prime}$，记属于图$\mathcal{G}$但不属于$\mathcal{G}^{\prime}$图的节点集合记为$\mathcal{V}/\mathcal{V}^{\prime}$，属于$\mathcal{V}^{\prime}$的任意节点对之间存在至少一条路径，但不存在一条边连接属于$\mathcal{V}^{\prime}$的节点与属于$\mathcal{V}/\mathcal{V}^{\prime}$的节点，则图$\mathcal{G}^{\prime}$是图$\mathcal{G}$的连通分量。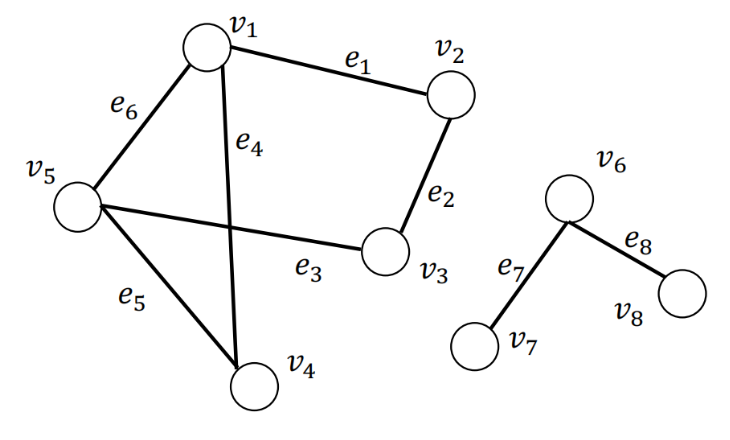
图4
左右两个子图都是整图的连通分量。

1.8 连通图(connected graph)

只包含一个连通分量(即其自身)的图是一个连通图。

1.9 最短路径(shortest path)

$v_{s}, v_{t} \in \mathcal{V}$ 是图$\mathcal{G}={\mathcal{V}, \mathcal{E}}$上的一对节点，节点对$v_{s}, v_{t} \in \mathcal{V}$之间所有路径集合$\mathcal{P}{\mathrm{st}}$。节点对$v{s}, v_{t}$之间的最短路径$p_{\mathrm{s} t}^{\mathrm{sp}}$为$\mathcal{P}{\mathrm{st}}$中长度最短的一条路径，即$p{\mathrm{s} t}^{\mathrm{sp}}=\arg \min {p \in \mathcal{P}{\mathrm{st}}}|p|$，$p$表示$\mathcal{P}_{\mathrm{st}}$中的一条路径，$|p|$是路径$p$的长度(边数量×权重)。

1.10 直径(diameter)

一个连通图$\mathcal{G}={\mathcal{V}, \mathcal{E}}$中，其直径为其所有节点对之间的最短路径的最大值，即$\operatorname{diameter}(\mathcal{G})=\max {v{s}, v_{t} \in \mathcal{V}} \min {p \in \mathcal{P}{s t}}|p|$

1.11 拉普拉斯矩阵(Laplacian Matrix)

图$\mathcal{G}={\mathcal{V}, \mathcal{E}}$，其邻接矩阵为$A$，其拉普拉斯矩阵定义为$\mathbf{L=D-A}$，其中$\mathbf{D=diag(d(v_1), \cdots, d(v_N))}$。

1.12 对称归一化的拉普拉斯矩阵(Symmetric normalized Laplacian)

图$\mathcal{G}={\mathcal{V}, \mathcal{E}}$，其邻接矩阵为$A$，其规范化的拉普拉斯矩阵定义为$\mathbf{L=D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}}$。

2. 图结构数据上的机器学习

节点预测：预测节点的类别或某类属性的取值。
边预测：预测两个节点间是否存在链接。
图预测：对不同的图进行分类或预测图的属性。
节点聚类：检测节点是否形成一个类。

3. 环境配置

PyTorch Geometric (PyG)是面向几何深度学习的PyTorch的扩展库，基于PyG库，我们可以轻松地根据数据生成一个图对象。

3.1 安装的pytorch和cudatoolkit
1
conda install pytorch torchvision torchaudio cudatoolkit=11.1 -c pytorch -c nvidia

安装成功后可以验证一下。

1
2
3
import torch
print(torch.__version__)
print(torch.version.cuda)
3.2 安装PyG
1
2
3
4
5
pip install torch-scatter -f https://pytorch-geometric.com/whl/torch-1.8.0+cu111.html
pip install torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+cu111.html
pip install torch-cluster -f https://pytorch-geometric.com/whl/torch-1.8.0+cu111.html
pip install torch-spline-conv -f https://pytorch-geometric.com/whl/torch-1.8.0+cu111.html
pip install torch-geometric

4. Data类——PyG中图的表示

4.1 构造函数
1
2
3
4
5
6
7
8
9
10
11
12
class Data(object):
    def __init__(self, x=None, edge_index=None, edge_attr=None, y=None, **kwargs):
    self.x = x
    self.edge_index = edge_index
    self.edge_attr = edge_attr
    self.y = y

    for key, item in kwargs.items():
        if key == 'num_nodes':
            self.__num_nodes__ = item
        else:
            self[key] = item

Args:
· x (Tensor, optional): 节点属性矩阵，大小为[num_nodes, num_node_features]
· edge_index (LongTensor, optional): 边索引矩阵，大小为[2, num_edges]，第0行为尾节点，第1行为头节点，头指向尾。
· edge_attr (Tensor, optional): 边属性矩阵，大小为[num_edges, num_edge_features]
· y (Tensor, optional): 节点或图的标签，任意大小(其实也可以是边的标签)

4.2 参数

一个图至少包含x, edge_index, edge_attr, y, num_nodes5个属性，也可以指定额外参数使Data对象包含其他的属性：

1
graph = Data(x=x, edge_index=edge_index, edge_attr=edge_attr, y=y, num_nodes=num_nodes, other_attr=other_attr)
4.3 Data对象与其他数据互转
1
2
3
4
5
6
7
8
9
10
#dict to Data
graph_dict = {
    'x': x,
    'edge_index': edge_index,
    'edge_attr': edge_attr,
    'y': y,
    'num_nodes': num_nodes,
    'other_attr': other_attr
}
graph_data = Data.from_dict(graph_dict)
1
2
3
#Data to dict
def Data_to_dict(self):
    return {key: item for key, item in self}
1
2
3
4
5
#Data to namedtuple
def Data_to_namedtuple(self):
    keys = self.keys
    DataTuple = collections.namedtuple('DataTuple', keys)
    return DataTuple(*[self[key] for key in keys])
4.4 Data对象属性
1
2
#获取Data对象属性
x = graph_data['x']
1
2
#获取Data对象属性关键字
graph_data.keys()
1
2
#对边排序并移除重复的边
graph_data.coalesce()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from torch_geometric.datasets import KarateClub
dataset = KarateClub()
data = dataset[0]

print(data.num_nodes) #节点数量
print(data.num_edges) #边数量
print(data.num_node_features) #节点属性维度
print(data.num_edge_features) #边属性维度
print(data.num_edges/data.num_nodes) #平均节点度
print(data.is_coalesced()) #是否边是有序的同时不含有重复的边
print(data.train_mask.sum()) #用作训练集的节点
print(int(data.train_mask.sum())/data.num_nodes) #用作训练集的节点数占比
print(data.contains_isolated_nodes()) #此图是否包含孤立的节点
print(data.contains_self_loops()) #此图是否包含自环的边
print(data.is_undirected()) #此图是否是无向图

5.Dataset类——PyG中图数据集的表示

5.1 数据集的下载

首先下载PyG内置的Planetoid数据集

1
2
3
4
5
6
from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='/dataset/Cora', name='Cora')

print(len(dataset))    #数据集中图的数量
print(dataset.num_classes)   #分类任务的数量
print(dataset.num_node_features)   ##节点属性维度
5.1 数据集的使用

定义一个名为Net的图神经网络模型，将节点分类图数据集加入训练。

1
2
3
4
5
6
7
8
9
10
11
model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

model.train()
for epoch in range(500):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

1.datawhale-GNN开源学习资料

欢迎关注我们的公众号
0%