一般情况下,可以把异常检测看成是数据不平衡下的分类问题,如果数据条件允许,优先使用有监督异常检测如XGBOOST;仅有少量标签时,可以用无监督学习作为一种特征抽取方式,最后喂给有监督的分类模型。
之前介绍的统计与概率模型、线性模型、基于相似度的模型,和今天要介绍的集成学习都是无监督模型。
为什么要使用集成学习?——①适合高维度数据(空间稀疏),②提高模型鲁棒性。
值得注意的时,异常检测没有标签,所以feature bagging、bagging比boosting多。而使用boosting进行异常检测,需要生成伪标签。
1. Feature Bagging
Feature Bagging,基本思想与bagging相似,只是对象是feature。
基本检测器可以彼此完全不同,或不同的参数设置,或使用不同采样的子数据集。Feature bagging常用lof算法为基算法。
1.1 算法原理

1.2 不同检测器的分数标准化
不同检测器可能会在不同的尺度上产生分数。例如,平均k近邻检测器会输出原始距离分数,而LOF算法会输出归一化值。另外,检测器输出的异常值分数大小不一,因此需要归一化,常见方法包括平均和最大化组合函数。
以累积求和法和广度优先法为例,简单介绍下:
①累积求和:针对每组样本,分别累加对应的全部基本检测器的结果;共输出T组求和结果。
②广度优先:枚举每一种基本检测器(共m种),再嵌套枚举每一组异常值输出(共T种),每种异常检测算法分别检测T组样本数据,共有m*T种组合,按照广度优先搜索,先到先占位,重复数据取后来的异常值的最大值、平均值等。
1.3 Feature Bagging的缺陷
①bagging有放回抽样,会损失部分特征的信息,或者特征始终无法被采样也无法被模型训练到。因此使用bagging实际上需要处理偏差和方差之间的一种微妙的均衡。
②bagging的比例通常在0.5到0.99之间,如果存在过多的相关性特征,会导致泛化能力下降。所以进行异常检测之前,必须进行严格的相关性分析或者主成分分析。
2. Isolation Forest
周志华老师在2008年提出的算法,在工业界应用广泛,其不需要定义数学模型也不需要训练数据有标签。
这种算法在全局和局部都通过采样引入了随机性,往往要比单纯的feature bagging的效果更好。
2.1 关于异常的定义
使用孤立森林(Isolation Forests)的前提是,将异常点定义为那些 “容易被孤立的离群点” —— 可以理解为分布稀疏,且距离高密度群体较远的点。即默认①异常数据占总样本量的比例很小,②异常点的特征值与正常点的差异很大。
2.2 查找孤立点的策略
用一个随机超平面来切割数据空间,切一次可以生成两个子空间。继续用随机超平面来切割每个子空间并循环,直到每个子空间只有一个数据点为止。
以二维空间作为演示,点B’跟其他数据点比较疏离,只需要很少的几次操作就可以将它细分出来;点A’需要的切分次数会更多一些。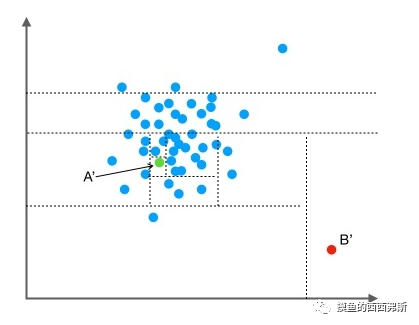
2.3 树的构造方法
训练:构建一棵 iTree 时,先从全量数据中抽取一批样本,然后随机选择一个特征作为起始节点,并在该特征的最大值和最小值之间随机选择一个值,将样本中小于该取值的数据划到左分支,大于等于该取值的划到右分支。然后,在左右两个分支数据中,重复上述步骤,直到满足如下条件:①数据不可再分,即:只包含一条数据,或者全部数据相同。②二叉树达到限定的最大深度。
预测:计算数据 x 的异常分值时,先要估算它在每棵 iTree 中的路径深度。先沿着一棵 iTree,从根节点开始按不同特征的取值从上往下,直到到达某叶子节点。假设 iTree 的训练样本中同样落在 x 所在叶子节点的样本数为 T.size,则数据 x 在这棵 iTree 上的路径深度 h(x),可以用下面这个公式计算:
$$
h\left( x \right) =e+C\left( T.size \right)
$$
式中,e 表示数据 x 从 iTree 的根节点到叶节点过程中经过的边的数目,C(T.size) 可以认为是一个修正值,它表示在一棵用 T.size 条样本数据构建的二叉树的平均路径长度。C(n) 的计算公式如下:
$$
C\left( n \right) =2H\left( n-1 \right) -\frac{2\left( n-1 \right)}{n}
$$
其中,H(n-1) 可用 ln(n-1)+0.5772156649(欧拉常数)估算。数据 x 最终的异常分值 Score(x) 综合了多棵 iTree 的结果:
$$
Score\left( x \right) =2^{-\frac{E\left( h\left( x \right) \right)}{C\left( \varPsi \right)}}
$$
公式中,E(h(x)) 表示数据 x 在多棵 iTree 的路径长度的均值,ψ表示单棵 iTree 的训练样本的样本数,C(ψ)表示用ψ条数据构建的二叉树的平均路径长度,它在这里主要用来做归一化。
从异常分值的公式看,如果数据 x 在多棵 iTree 中的平均路径长度越短,得分越接近 1,表明数据 x 越异常;如果数据 x 在多棵 iTree 中的平均路径长度越长,得分越接近 0,表示数据 x 越正常;如果数据 x 在多棵 iTree 中的平均路径长度接近整体均值,则打分会在 0.5 附近。
在实际情况中,不同模型在不同的数据集上表现不一。但是总体而言KNN等基于位置和距离度量的算法原理不太复杂,表现也较为稳定。
唯一的缺点是,KNN等基于距离度量模型受到数据维度的影响较大,当维度比较低时表现很好。如果异常特征隐藏在少数维度上时,KNN和LOF类的效果就不会太好,此时该选择Isolation Forest(适合高维空间)。
