异常值通常具有更高的离群程度分数值,同时也更具有可解释性。在基于相似度的异常检测方法中,主要思想是异常点的表示与正常点不同。
1. 基于距离的度量
基于距离的异常检测有这样一个前提假设,即异常点的k近邻距离要远大于正常点。常见的方法是嵌套循环,第一层循环遍历每个数据,第二层循环进行异常判断计算当前点与其他点的距离,一旦发现多于k个数据点与当前点的距离在D之内,则将该点标记为非异常值。 此法计算的时间复杂度为O(N2),当数据量比较大时需要修剪方法以加快距离计算。
1.1 基于单元的方法
在基于单元格的技术中,数据空间被划分为单元格,单元格的宽度是阈值D和数据维数d的函数。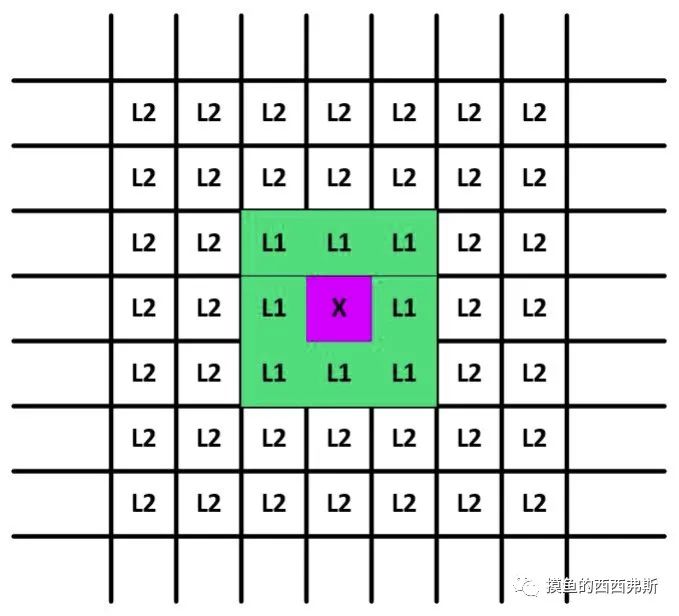
L1邻居表示通过最多1个单元间的边界可从该单元到达的单元格的集合,L2邻居表示通过跨越2个或3个边界而获得的那些单元格。
以二维数据为例,网格间的距离为D/2√d,其具有以下性质:
①单元格中两点之间的距离最多为D/2 。
②一个点与L1邻接点之间的距离最大为D。
③一个点与它的Lr邻居(其中r>2)中的一个点之间的距离至少为D。
但是L2中并不能直接得出结论,需要另外定义规则,如:
①如果一个单元格中包含超过k个数据点及其L1邻居,那么这些数据点都不是异常值。
②如果单元A及其相邻L1和L2中包含少于k个数据点,则单元A中的所有点都是异常值。
利用第二条规则的修剪能力,对于包含至少一个数据点的每个单元格A,计算其中的点数及其L1和L2邻居的总和。 如果该数字不超过k,则将单元格A中的所有点标记为离群值。
对于此时仍未标记为异常值或非异常值的单元格中的数据点,需要明确计算其k最近邻距离,在L1和L2中不超过k个且距离小于D的数据点,则声明为异常值。
1.2 基于索引的方法
对于一个给定数据集,基于索引的方法利用多维索引结构(如R树、k-d树)来搜索每个数据对象A在半径范围D内的相邻点。设M是一个异常值在其D-邻域内允许含有对象数的最大值,若发现某个数据对象A的D-邻域内出现M+1甚至更多个相邻点, 则判定对象A不是异常值。该算法时间复杂度在最坏情况下为O(kN2),其中k是数据集维数,N是数据集包含对象的个数。但是构造索引的任务本身也需要密集复杂的计算量。
2. 基于密度的度量
基于密度的算法主要有局部离群因子(LocalOutlierFactor,LOF),以及LOCI、CLOF等基于LOF的改进算法。LOF的关键步骤在于给每个数据点都分配一个离散度,其主要思想是:针对给定的数据集,对其中的任意一个数据点,如果在其局部邻域内的点都很密集,那么认为此数据点为正常数据点;而离群点则是距离正常数据点最近邻的点都比较远的数据点。
2.1 k-距离
类似k近邻的思路,首先定义一个k-距离,对于数据集D中的给定对象p,对象p与数据集D中任意点o的距离为d(po)。我们把数据集D中与对象p距离最近的k个相邻点的最远距离表示为k-distance(p),把距离对象p距离第k近的点表示为ok,那么给定对象p和点ok之间的距离d(p,ok)=k-distance(p),满足:
①在集合D中至少有不包括p在内的k个点 o’,其中o’∈D \ {p},满足d(p,o’)≤d(p,ok)
②在集合D中最多有不包括p在内的k-1个点o’,其中o’∈D \ {p},满足d(p,o’)<d(pok)
直观一些理解,就是以对象p为中心,对数据集D中的所有点到p的距离进行排序,距离对象p第k近的点ok与p之间的距离就是k-距离。
2.2 k-邻域
到对象p的距离小于等于k-距离的所有点的集合就是k-邻域:
$$
N_{k-dis\tan ce\left(p \right)}\left(p \right) =\left{ q\in D\backslash{q}\left| d\left(p,d \right) \right. \le k-ds\tan ce\left(p \right) \right}
$$
k-邻域包含对象p的第k距离以内的所有点,包括第k距离点;对象p的第k邻域点的个数丨Nk(p)≥3丨。
在二维平面上展示,对象p的k-邻域是以对象p为圆心、k-距离为半径围成的圆形区域。
2.3 可达距离
按照到对象o的距离远近,将数据集D内的点按照到o 的距离分为两类:
①若pi在对象o的k-邻域内,则可达距离就是给定点pi关于对象o的k-距离;
②若pi在对象o的k-邻域外,则可达距离就是给定点pi关于对象o的实际距离。
给定点pi关于对象o的可达距离用数学公式可以表示为:
$$
r e a c h−d i s t_ k (p,o) = max {k−distance(o),d (p,o)}
$$
这样的分类处理可以简化后续的计算,同时让得到的数值区分度更高。
如图所示:
①p1在对象o的k-邻域内,d(p1,o)<k−distance(o),
可达距离reach−distk(p1,o)=k−distance(o) ;
②p2在对象o的k-邻域外,d (p2,o)>k−distance(o),
可达距离reach−distk(p2,o)= d(p2,o) ;
需要注意的是:为了减少距离的计算开销,对象的k-邻域内的所有对象的k-距离计算量可以被显著降低,相当于使用一个阈值把需要计算的部分“截断”了, 的值越高,无需计算的邻近点越多,计算开销越小。但是另一方面,k的值变高,可能意味着可达距离变远,对集群点和离群点的区分度可能变低。因此,如何选择k值,是LOF算法能否达到效率与效果平衡的重要因素。
3.4 局部可达密度
可以将“密度”直观地理解为点的聚集程度,简单来说,点与点之间距离越短,则密度越大。我们使用数据集D中对象p与对象o的k-邻域内所有点的可达距离平均值的倒数来定义局部可达密度。
在进行局部可达密度的计算的时候,我们需要避免数据集内所有数据落在同一点上,即所有可达距离之和为0的情况:此时局部密度为∞,后续计算将无法进行。
LOF算法中针对这一问题进行了如下的定义:对于数据集D内的给定对象p,存在至少MinPts(p)≥1个不同于p的点。因此,我们使用对象p到o∈N_{MinPts}(p)的可达距离reach-dist{MinPts}(p, o)作为度量对象p邻域的密度的值。点p的局部可达密度计算公式为:
$$
lrd_{MinPts}(p)=1/(\frac {\sum\limits_{o∈N_{MinPts}(p)} reach-dist_{MinPts}(p,o)} {\left\vert N_{MinPts}(p) \right\vert})
$$
由公式可看出,这里是对给定点p进行度量,计算其邻域内的所有对象o到给定点p的可达距离平均值。给定点p的局部可达密度越高,越可能与其邻域内的点p属于同一簇;密度越低,越可能是离群点。
3.5 局部异常因子
得到lrd(局部可达密度)以后就可以将每个点的lrd将与它们的k个邻点的lrd进行比较,得到局部异常因子LOF。 LOF是对象p的邻居点o(o∈NMinPts(p))的lrd平均值与p的lrd的比值。
p的局部可达密度越低,且它的MinPts近邻的平均局部可达密度越高,则p的LOF值越高。如果这个比值越接近1,说明o的邻域点密度差不多,o可能和邻域同属一簇;如果这个比值小于1,说明o的密度高于其邻域点密度,o为密集点;如果这个比值大于1,说明o的密度小于其邻域点密度,o可能是异常点。
由上述公式计算出的LOF数值,就是我们所需要的离群点分数。


