异常检测——线性相关方法

Posted on | In |
Words count in article: 2.2k

真实数据集中不同维度的特征可能具有高度相关性，这是因为不同的特征往往是由相同的基础过程以密切相关的方式产生的。这被称为——回归建模，是一种参数化的相关性分析。
一类相关性分析通过其他变量预测单独的属性值，另一类方法用一些潜在变量来代表整个数
据。前者的代表是线性回归，后者一个典型的例子是主成分分析。
线性相关分析基于的假设是：①近似线性相关假设；②子空间假设。为了确定线性模型是否适合数据集，需要进行探索性和可视化分析。

0. 探索性和可视化分析

1
2
train_data.describe()
train_data.info()
1
2
3
4
5
6
7
8
9
#相关性分析
numeric_features = ['f'+str(i) for i in range(20)]
numeric = train_data[numeric_features]
correlation.numeric.corr()

f,ax = plt.subplots(figsize=(15,15))
sns.heatmap(correlation,square=True)
plt.tile('Correlation of Numeric features',y=1,size=16)
plt.show()

xx

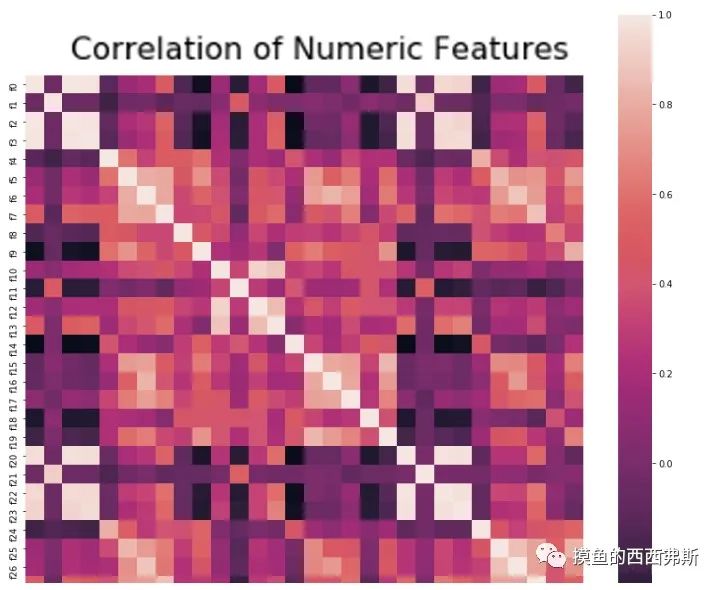
1. 线性回归

线性回归：假设不同维度的变量具有一定的相关性，并可以通过一个相关系数矩阵进行衡量。
在线性回归中，异常值是根据自变量对因变量的影响来定义的，自变量之间相互关系中的异常则不那么重要。(此处的异常点检测是基于数据点的整体分布)

1.1 最小二乘法

基于最小二乘拟合的线性回归可以如下定义：带标签数据集
$$
D=\left{ \left( x_1,y_1 \right) ,…,\left( x_m,y_m \right) \right}
$$
m个样本的特征组成矩阵X；m个样本的标签组成标签向量
$$
y=\left( y_1,…,y_m \right) ^T
$$
目的是求出θ，使得目标函数J(θ)最小。
$$
J\left( \theta \right) =\lVert \left. X\theta -y \rVert {2}^{2} \right.
$$
为什么目标函数J(θ)是残差向量的2-范数的平方？可以这样解释：
某个样本(xi,yi)在θ确定情况下满足：
$$
y_i=\theta ^Tx_i+\epsilon i
$$
ϵi为误差项，可以看作独立同分布的随机变量，且服从高斯分布。可以以计算yi的概率密度函数：
$$
L\left( \theta \right) =p\left( y_i\left| x_i;\theta \right. \right) =\frac{1}{\sqrt{2\pi}\sigma}\exp \left( -\frac{\left( y_i-\theta ^Tx_i \right) ^2}{2\sigma ^2} \right)
$$
要使J(θ)最小，就要使使L(θ)最大，可使用最大似然估计法。
$$
L\left( \theta \right) =\log \prod{i=1}^m{\frac{1}{\sqrt{2\pi}\sigma}\exp \left( -\frac{\left( y_i-\theta ^Tx_i \right) ^2}{2\sigma ^2} \right)}=m\log \frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma ^2}·\frac{1}{2}\sum{i-=1}^m{\left( y_i-\theta ^Tx_i \right)}^2
$$
通常做法是对似然函数求导，使导数为0。上述也证明了要让L(θ)最大就是要让J(θ)最小。
$$
\sum_{i-=1}^m{\left( y_i-\theta ^Tx_i \right)}^2=\lVert \left. X\theta -y \rVert \right. _{2}^{2}
$$
说回最小二乘，目的是求出最优点θ使J(θ)最小。
设残差向量r=Xθ−y，在二维空间中讨论，Xθ为一条直线，y为一个向量，存在最优点θ✲使得J(θ)最小，这个θ✲是最小二乘解集合中的一个元素，如图所示：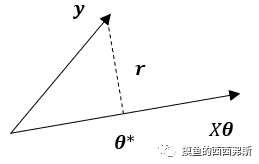
xx
由图看出这个θ✲是r垂直于Xθ时取到。由定义，Xθ是矩阵X的列空间C(X)，与C(X)垂直的是矩阵X的左零空间N(XT)，由左零空间定义：
$$
X^Tr=0
$$
把r=Xθ−y带入，得到：
$$
X^T\left( X\theta -y \right) =0
$$
整理得最优参数θ为：
$$
\theta =\left( X^T·X \right) ^{-1}·\left( X^T·y \right)
$$
个人觉得J(θ)也可以认为是某种异常得分。

1.2 梯度下降

线性回归的优化目标是损失函数，就需要一种优化算法。
线性回归中的常用损失函数是均方误差MSE，表达式为：
$$
L\left( w,b \right) =\frac{1}{2}\left( \hat{y}^{\left( i \right)}-y^{\left( i \right)} \right) ^2 = \frac{1}{n}\sum_{i=1}^n{l^{\left( i \right)}}\left( w,b \right) =\frac{1}{n}\sum_{i=1}{\frac{1}{2}\left( W^Tx^{\left( i \right)}+b-y^{\left( i \right)} \right)}^2
$$
当模型和损失函数形式较为简单时，面的误差最小化问题的解可以直接用公式表达出来。然而，大多数深度学习模型并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。
在求数值解的优化算法中，小批量随机梯度下降（mini-batch stochastic gradient descent）被广泛使用。他的算法是：先选取一组模型参数的初始值，如随机选取；接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量（mini-batch），然后求小批量中数据样本的平均损失和有关模型参数的导数（梯度），最后用此结果与预先设定的学习率的乘积作为模型参数在本次迭代的减小量。如下式所示：
$$
\left( w,b \right) \gets \left( w,b \right) -\frac{\eta}{\left| \left. \mathbb{B} \right| \right.}\sum_{i\in \mathbb{B}}{\partial _{\left( w,b \right)}}l^{\left( i \right)}\left( w,b \right)
$$
B表示批量大小batch size；η表示学习率，代表每次学习的步长大小。

2. 主成分分析

最小二乘法试图找到一个与数据具有最佳匹配(d-1)维超平面；主成分分析方法可用于解决这一问题的广义版本，它可以找到任意k(k<d)维的最优表示超平面，从而使平方投
影误差最小化。

2.1 原理

对于d维，包含N个样本的数据，用Ri表示其中第i行[xi1,…xid]，可得到d×d的协方差矩阵：
$$
\sum{=\left( R-\bar{R} \right)}^T·\left( R-\bar{R} \right)
$$
∑是对称并且半正定的，因此可以进行相似对角化：
$$
\sum{=P·D·P^T}
$$
这里的D为对角矩阵，对角元素为特征值。P为标准正交矩阵，每一行为对应的特征向量；这些标准正交向量提供了数据应该投影的轴线方向。
将样本的协方差矩阵特征值分解以后，特征值就是样本投影到这个轴上后对应的方差，特征值越小，说明投影以后在这个轴上样本点分布集中，而异常点在这种情况下更容易偏移，利用这一点可以作为衡量样本异常的一个指标。在PCA做降维的时候，起作用的是大的特征值对应的特征向量，而在异常检测中，起作用的是特征值小的对应的特征向量。根据以上思想，我们可以定义PCA中一个点x的异常评分：
$$
Score\left( x \right) =\sum_{i=1}^d{\frac{\left| \left. x^Te_i \right| \right.}{\lambda _i}}
$$
其中，ei为第i个特征向量，λ为沿该方向的方差(也是特征值)，可以看出对异常得分的大部分贡献是由λ值较小的主成分的提供的。

2.2 PyOD实例

测试PCA和HBOS的性能对比。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from sklearn.model_selection import train_test_split
from pyod.models.pca import PCA
from pyod.models.hbos import HBOS
from pyod.utils.data import evaluate_print
import pandas as pd
import numpy as np

if __name__ == "__main__":
    data = pd.read_csv('dataverse_files/breast-cancer-unsupervised-ad.csv', header=None)
    data_x=data[[i for i in range(30)]].values #特征
    data_y=data[30].map(lambda x: 1 if x=='o' else 0).values #标签
    X_train, X_test, y_train, y_test = train_test_split(data_x, data_y, test_size=0.3,stratify=data_y)#使用分层抽样，构建训练集和测试集
    train_number=X_train.shape[0]#训练集样本的个数

	#PCA方法
    clf1 = PCA(n_components=15)
    clf1.fit(X_train)
    y_train_scores_clf1 = clf1.decision_scores_
    y_test_scores_clf1 = clf1.decision_function(X_test)

	#HBOS方法
    clf2 = HBOS(n_bins=(int)(np.sqrt(train_number)))
    clf2.fit(X_train)
    y_train_scores_clf2 = clf2.decision_scores_
    y_test_scores_clf2 = clf2.decision_function(X_test)

	#结果对比
    print("Training Data:")
    evaluate_print('PCA', y_train, y_train_scores_clf1)
    evaluate_print('HBOS', y_train, y_train_scores_clf2)

    print("Test Data:")
    evaluate_print('PCA', y_test, y_test_scores_clf1)
    evaluate_print('HBOS', y_test, y_test_scores_clf2)

结果发现，PCA的性能优于HBOS。

局限性:
1.回归分析作为检测离群值的工具有一些局限性：为了使回归分析技术有效，数据需要高度相关，并沿着低维子空间对齐。当数据不相关，但在某些区域高度聚集时，这种方法可能不会有效。
2.数据中的相关性在本质上可能不是全局性的。子空间相关性可能是特定于数
据的特定位置的。在这种情况下，由主成分分析发现的全局子空间对于异常检测是次优的。因此，为了创建更一般的局部子空间模型，有时将线性模型与邻近模型结合起来是有用的。

参考资料

1.datawhale-异常检测开源学习资料

欢迎关注我们的公众号
0%