异常检测的统计方法包含两种主要类型：参数方法和非参数方法。
参数方法：假定数据服从以θ为参数的参数分布，该参数分布的概率密度函数f(x,θ)给出x属于该分布的概率，该值越小，x越可能是异常点。(仅对数据做的统计假定满足实际约束时可行)
非参数方法：不假定先验统计模型，假定参数的个数较为灵活，并非完全无参。
1. 参数方法
1.1 基于正态分布的一元异常点检测
仅涉及单变量的数据称为一元数据，假定数据由正态分布产生，由输入数据学习正态分布的参数，并把低概率的点识别为异常点。
输入数据集
，根据公式可以求出参数均值μ和方差σ，和概率密度函数p(x)。
$$
\mu =\frac{1}{n}\sum_{i=1}^n{x_i}
$$
$$
\sigma ^2=\frac{1}{n}\sum_{i=1}^n{\left( x_i-\mu \right)}^2
$$
$$
p\left( x \right) =\frac{1}{\sqrt{2\pi}\sigma}\exp \left( -\frac{\left( x-\mu \right) ^2}{2\sigma ^2} \right)
$$
在正太分布的假设中，可以为p(x)取值设置阈值来判断异常点。
或者简单地用3σ法则来判断，(μ-3σ，μ+3σ)包含99.7%的数据，某数据超出这个范围，可以简单的标记为异常点(Outlier)。
1.2 多元离群点的检测方法
一元异常点检测的方法可以扩展为多元异常点检测。
对于一个n维数据集合
，当各个维度的特征之间相互独立，可以按上述公式计算每个维度的均值和方差。基于正态分布的假设，根据概率
的大小判断x是否属于异常值。
$$
p\left(\vec{x} \right) =\prod_{j=1}^n{p\left(x_j;\mu _j;\sigma {j}^{2} \right)}=\prod{j=1}^n{\frac{1}{\sqrt{2\pi}\sigma _j}}\exp \left(-\frac{\left(x_j-\mu j \right) ^2}{2\sigma {j}^{2}} \right)
$$
当各个维度的特征相关时，需要用到基于多元正太分布来进行异常点检测，首先计算n维的均值向量
$$
\vec{\mu}=\left( E\left( x_1 \right) ,…,E\left( x_n \right) \right)
$$
和n×n的协方差矩阵：
$$
\sum{=\frac{1}{m}}\sum{i=1}^m{\left( \vec{x}-\vec{\mu} \right) \left( \vec{x}-\vec{\mu} \right) ^T}
$$
如有新数据，可以计算,根据概率值大小判断是否属于异常值。
$$
p\left( \vec{x} \right) =\frac{1}{\left( 2\pi ^{\frac{n}{2}}\left| \sum{} \right|^{{2}^{1}} \right)}\exp \left( -\frac{1}{2}\left( \vec{x}-\vec{\mu} \right) ^T\sum{^{-1}\left( \vec{x}-\vec{\mu} \right)} \right)
$$
2. 非参数方法
非参数方法是对数据做较少的假定，因而适合多数情况。
2.1 基于角度的方法
基于角度的方法往往在高维空间里会很有效，其主要思想是：数据边界上的数据很可能将整个数据包围在一个较小的角度内，而内部的数据点则可能以不同的角度围绕着他们。如下图所示，其中点A是一个异常点，点B位于数据内部。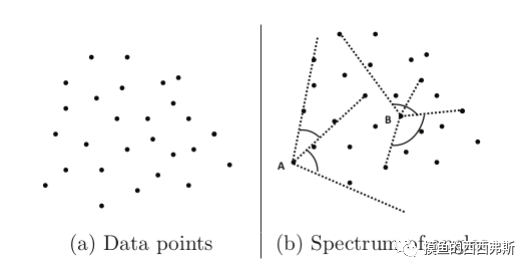
如果数据点与其余点离得较远，则潜在角度可能越小。因此，具有较小角度谱的数据点较有可能异常值，而具有较大角度谱的数据点不太可能是异常值。
2.2 基于频数直方图的无监督异常点检测算法(HBOS)
HBOS(Histogram-based Outlier Score)是一种单变量方法组合，HBOS在全局异常检测问题上表现良好，但不能检测局部异常值。但是HBOS比标准算法快得多，尤其是在大数据集上。
HOBS不能对特征之间的依赖关系进行建模，其基本假设是数据集的每个维度相互独立。然后对每个维度进行区间(bin)划分，对每一个bin进行评分。区间的密度越低，异常评分越高，越可能是异常点。
①等宽分桶：标准直方图构建，在值范围内构造k个等宽箱，样本若如每个箱的概率作为密度的估计[时间复杂度O(n)]
②动态宽度分桶：对所有值进行排序，将固定数量的N/k个连续值装进一个箱。N是总实例数，k是箱个数，所有箱面积一样，跨度大的箱的高度低，即密度小(例外情况：超过k个数相等，此时允许在同一个箱里超过N/k值)
对每个维度都计算一个独立的直方图，其中每个箱子的高度表示密度的估计，对直方图进行归一化处理，最后计算每一个实例的HBOS值。
$$
HBOS\left( p \right) =\sum_{i=0}^d{\log \left( \frac{1}{hist_i\left( p \right)} \right)}
$$
详细推导过程：
假设样本o的第i个特征概率密度为
，则o的概率密度为：
$$
P\left( p \right) =P_1\left( p \right) P_2\left( p \right) …P_d\left( p \right)
$$
两边取对数
$$
\log \left( P\left( p \right) \right) =\log \left( P_1\left( p \right) P_2\left( p \right) …P_d\left( p \right) \right) =\sum_{i=1}^d{\log \left( P_i\left( p \right) \right)}
$$
为了达到概率密度越大异常评分越小，两边同乘-1。
$$
-\log \left( P\left( p \right) \right) =-\sum_{i=1}^d{\log \left( P_i\left( p \right) \right)}=\sum_{i=1}^d{\frac{1}{\log \left( P_i\left( p \right) \right)}}
$$
最后：
$$
HOBS\left( p \right) =-\log \left( P\left( p \right) \right) =\sum_{i=1}^d{\frac{1}{\log \left( P_i\left( p \right) \right)}}
$$
